Interval linear systems

This paragraph presents an overview of functions for obtaining estimates of the set of solutions of interval linear systems.

Run the following commands to connect the necessary modules

>>> import intvalpy as ip
>>> import numpy as np

Variability of the solution

def ive(A, b, N=40)

When solving the system, we usually get many different estimates, equally suitable as answers to the problem and consistent with its data. It is the variability that characterizes how small or large this set is.

To get a quantitative measure, use the ive function:

Parameters:

• AInterval

  The input interval matrix of ISLAE, which can be either square or rectangular.

• bInterval

  The interval vector of the right part of the ISLAE.

• Nint, optional

  The number of corner matrices for which the conditionality is calculated. By default, N = 40.

Returns:

• outfloat

  A measure of the variability of an interval system of linear equations IVE.

Examples:

A randomized algorithm was used to speed up the calculations, so there is a chance that a non-optimal value will be found. To overcome this problem we can increase the value of the parameter N.

>>> A = ip.Interval([
        [[98, 100], [99, 101]],
        [[97, 99], [98, 100]],
        [[96, 98], [97, 99]]
    ])
>>> b = ip.Interval([[190, 210], [200, 220], [190, 210]])
>>> ip.linear.ive(A, b, N=60)
1.56304

For more information, see the article Shary S.P.

Метод граничных интервалов

В случае, когда появляется необходимость визуализировать множество решений системы линейных неравенств (или интервальную систему уравнений), а также получить все вершины множество, можно прибегнуть к методам решения проблемы перечисления вершин. Однако существующие реализации имеют ряд недостатков: работа только с квадратными системами, плохая обработка неограниченных множеств.

Основываясь на применении матрицы граничных интервалов был предложен метод граничных интервалов для исследования и визуализации полиэдральных множеств. Главными преимуществами данного подхода является возможность работать с неограниченными и тощими множествами решений, а также с линейными системами, когда количество уравнений отлично от количества неизвестных.

Для общего понимания работы алгоритма укажем его основные шаги:

1. Формирование матрицы граничных интервалов;
2. Изменение матрицы граничных интервалов с учётом окна отрисовки;
3. Построение упорядоченных вершин полиэдрального множества решений;
4. Вывод построенных вершин и (если надо) отрисовка полиэдра.

Двумерная визуализация линейной системы неравенств

Для работы с линейной системой алгебраических неравенств A x >= b, когда количество неизвестных равно двум, необходимо воспользоваться функций lineqs. В случае, если множество решений неограниченно, то алгоритм самостоятельно выберет границы отрисовки. Однако пользователь сам может указать их явным образом.

Parameters:

• A: float

  Матрица системы линейных алгебраических неравенств.

• b: float

  Вектор правой части системы линейных алгебраических неравенств.

• show: bool, optional

  Данный параметр отвечает за то будет ли показано множество решений. По умолчанию указано значение True, т.е. происходит отрисовка графика.

• title: str, optional

  Верхняя легенда графика.

• color: str, optional

  Цвет внутренней области множества решений.

• bounds: array_like, optional

  Границы отрисовочного окна. Первый элемент массива отвечает за нижние грани по осям OX и OY, а второй за верхние. Таким образом, для того, чтобы OX лежало в пределах [-2, 2], а OY в пределах [-3, 4], необходимо задать bounds как [[-2, -3], [2, 4]].

• alpha: float, optional

  Прозрачность графика.

• s: float, optional

  Насколько велики точки вершин.

• size: tuple, optional

  Размер отрисовочного окна.

• save: bool, optional

  Если значение True, то график сохраняется.

Returns:

• out: list

  Возвращается список упорядоченных вершин. В случае, если show = True, то график отрисовывается.

Examples:

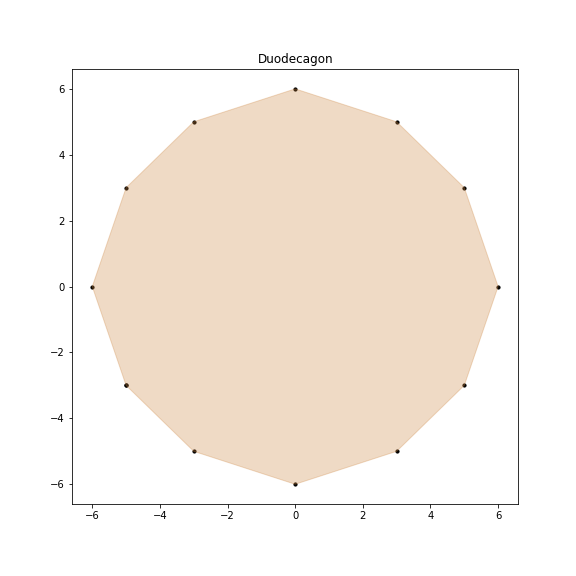
В качестве примера предлагается рассмотреть систему описывающую двенадцатиугольник:

>>> A = -np.array([[-3, -1],
>>>               [-2, -2],
>>>               [-1, -3],
>>>               [1, -3],
>>>               [2, -2],
>>>               [3, -1],
>>>               [3, 1],
>>>               [2, 2],
>>>               [1, 3],
>>>               [-1, 3],
>>>               [-2, 2],
>>>               [-3, 1]])
>>> b = -np.array([18,16,18,18,16,18,18,16,18,18,16,18])
>>> vertices = ip.lineqs(A, b, title='Duodecagon', color='peru', alpha=0.3, size=(8,8))
array([[-5., -3.], [-6., -0.], [-5.,  3.], [-3.,  5.], [-0.,  6.], [ 3.,  5.],
       [ 5.,  3.], [ 6.,  0.], [ 5., -3.], [ 3., -5.], [ 0., -6.], [-3., -5.]])

Трёхмерная визуализация линейной системы неравенств

Для работы с линейной системой алгебраических неравенств A x >= b, когда количество неизвестных равно трём, необходимо воспользоваться функций lineqs3D. В случае, если множество решений неограниченно, то алгоритм самостоятельно выберет границы отрисовки. Однако пользователь сам может указать их явным образом. Для понимания, что множество решений обрезано, плоскости окрашиваются в красный цвет.

Parameters:

• A: float

  Матрица системы линейных алгебраических неравенств.

• b: float

  Вектор правой части системы линейных алгебраических неравенств.

• show: bool, optional

  Данный параметр отвечает за то будет ли показано множество решений. По умолчанию указано значение True, т.е. происходит отрисовка графика.

• color: str, optional

  Цвет внутренней области множества решений.

• bounds: array_like, optional

  Границы отрисовочного окна. Первый элемент массива отвечает за нижние грани по осям OX, OY и OZ, а второй за верхние. Таким образом, для того, чтобы OX лежало в пределах [-2, 2], а OY в пределах [-3, 4], а OZ в пределах [1, 5] необходимо задать bounds как [[-2, -3, 1], [2, 4, 5]].

• alpha: float, optional

  Прозрачность графика.

• s: float, optional

  Насколько велики точки вершин.

• size: tuple, optional

  Размер отрисовочного окна.

Returns:

• out: list

  Возвращается список упорядоченных вершин. В случае, если show = True, то график отрисовывается.

Examples:

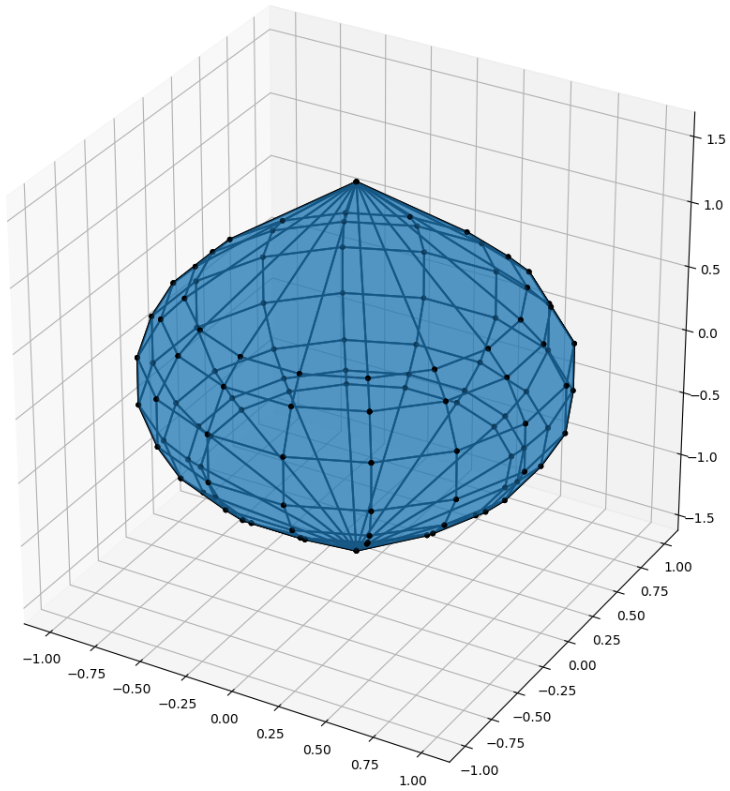
В качестве примера предлагается рассмотреть систему описывающую юлу:

>>> %matplotlib notebook
>>> k = 4
>>> A = []
>>> for alpha in np.arange(0, 2*np.pi - 0.0001, np.pi/(2*k)):
>>>     for beta in np.arange(-np.pi/2, np.pi/2, np.pi/(2*k)):
>>>         Ai = -np.array([np.sin(alpha), np.cos(alpha), np.sin(beta)])
>>>         Ai /= np.sqrt(Ai @ Ai)
>>>         A.append(Ai)
>>> A = np.array(A)
>>> b = -np.ones(A.shape[0])
>>>
>>> vertices = ip.lineqs3D(A, b)

Визуализация множества решений ИСЛАУ c двумя неизвестными

Для работы с интервальной линейной системой алгебраических уравнений A x = b, когда количество неизвестных равно двум, необходимо воспользоваться функций IntLinIncR2.

Для построения множества решений разобьём основную задачу на четыре подзадачи. Для этого воспользуемся свойством выпуклости решения в пересечении с каждым из ортантов пространства R², а также характеризацей Бекка. В результате получим задачи с системами линейных неравенств в каждом ортанте, которые можно визуализировать с помощью функции lineqs.

В случае, если множество решений неограниченно, то алгоритм самостоятельно выберет границы отрисовки. Однако пользователь сам может указать их явным образом.

Parameters:

• AInterval

  Входная интервальная матрица ИСЛАУ, которая может быть как квадратной, так и прямоугольной.

• bInterval

  Интервальной вектор правой части ИСЛАУ.

• show: bool, optional

  Данный параметр отвечает за то будет ли показано множество решений. По умолчанию указано значение True, т.е. происходит отрисовка графика.

• title: str, optional

  Верхняя легенда графика.

• consistency: str, optional

  Параметр для выбора типа множества решений. В случае, если он равен consistency = „uni“, то функция возвращает объединённое множество решение, если consistency = „tol“, то допусковое.

• bounds: array_like, optional

  Границы отрисовочного окна. Первый элемент массива отвечает за нижние грани по осям OX и OY, а второй за верхние. Таким образом, для того, чтобы OX лежало в пределах [-2, 2], а OY в пределах [-3, 4], необходимо задать bounds как [[-2, -3], [2, 4]].

• color: str, optional

  Цвет внутренней области множества решений.

• alpha: float, optional

  Прозрачность графика.

• s: float, optional

  Насколько велики точки вершин.

• size: tuple, optional

  Размер отрисовочного окна.

• save: bool, optional

  Если значение True, то график сохраняется.

Returns:

• out: list

  Возвращается список упорядоченных вершин в каждом ортанте начиная с первого и совершая обход в положительном направлении. В случае, если show = True, то график отрисовывается.

Examples:

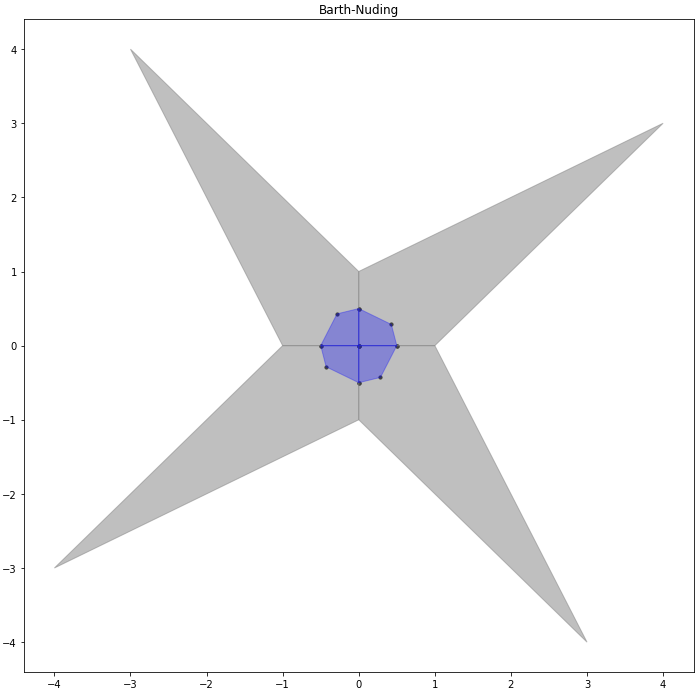
В качестве примера предлагается рассмотреть широкоизвестную интервальную систему предложенную Бартом-Нудингом. Для наглядности насколько отличаются разные типы решений изобразим на одном графике объединённое и допусковое множества:

>>> import matplotlib.pyplot as plt
>>>
>>> A = ip.Interval([[2, -2],[-1, 2]], [[4,1],[2,4]])
>>> b = ip.Interval([-2, -2], [2, 2])
>>>
>>> fig = plt.figure(figsize=(12,12))
>>> ax = fig.add_subplot(111, title='Barth-Nuding')
>>>
>>> vertices1 = ip.IntLinIncR2(A, b, show=False)
>>> vertices2 = ip.IntLinIncR2(A, b, consistency='tol', show=False)
>>>
>>> for v in vertices1:
>>>     # если пересечение с ортантом не пусто
>>>     if len(v) > 0:
>>>         x, y = v[:,0], v[:,1]
>>>         ax.fill(x, y, linestyle = '-', linewidth = 1, color='gray', alpha=0.5)
>>>         ax.scatter(x, y, s=0, color='black', alpha=1)
>>>
>>> for v in vertices2:
>>>     # если пересечение с ортантом не пусто
>>>     if len(v) > 0:
>>>         x, y = v[:,0], v[:,1]
>>>         ax.fill(x, y, linestyle = '-', linewidth = 1, color='blue', alpha=0.3)
>>>         ax.scatter(x, y, s=10, color='black', alpha=1)

Визуализация множества решений ИСЛАУ c тремя неизвестными

Для работы с интервальной линейной системой алгебраических уравнений A x = b, когда количество неизвестных равно трём, необходимо воспользоваться функций IntLinIncR3.

Для построения множества решений разобьём основную задачу на восемь подзадач. Для этого воспользуемся свойством выпуклости решения в пересечении с каждым из ортантов пространства R³, а также характеризацей Бекка. В результате получим задачи с системами линейных неравенств в каждом ортанте, которые можно визуализировать с помощью функции lineqs3D.

В случае, если множество решений неограниченно, то алгоритм самостоятельно выберет границы отрисовки. Однако пользователь сам может указать их явным образом. Для понимания, что множество решений обрезано, плоскости окрашиваются в красный цвет.

Parameters:

• AInterval

  Входная интервальная матрица ИСЛАУ, которая может быть как квадратной, так и прямоугольной.

• bInterval

  Интервальной вектор правой части ИСЛАУ.

• show: bool, optional

  Данный параметр отвечает за то будет ли показано множество решений. По умолчанию указано значение True, т.е. происходит отрисовка графика.

• consistency: str, optional

  Параметр для выбора типа множества решений. В случае, если он равен consistency = „uni“, то функция возвращает объединённое множество решение, если consistency = „tol“, то допусковое.

• bounds: array_like, optional

  Границы отрисовочного окна. Первый элемент массива отвечает за нижние грани по осям OX, OY и OZ, а второй за верхние. Таким образом, для того, чтобы OX лежало в пределах [-2, 2], а OY в пределах [-3, 4], а OZ в пределах [1, 5] необходимо задать bounds как [[-2, -3, 1], [2, 4, 5]].

• color: str, optional

  Цвет внутренней области множества решений.

• alpha: float, optional

  Прозрачность графика.

• s: float, optional

  Насколько велики точки вершин.

• size: tuple, optional

  Размер отрисовочного окна.

Returns:

• out: list

  Возвращается список упорядоченных вершин в каждом ортанте. В случае, если show = True, то график отрисовывается.

Examples:

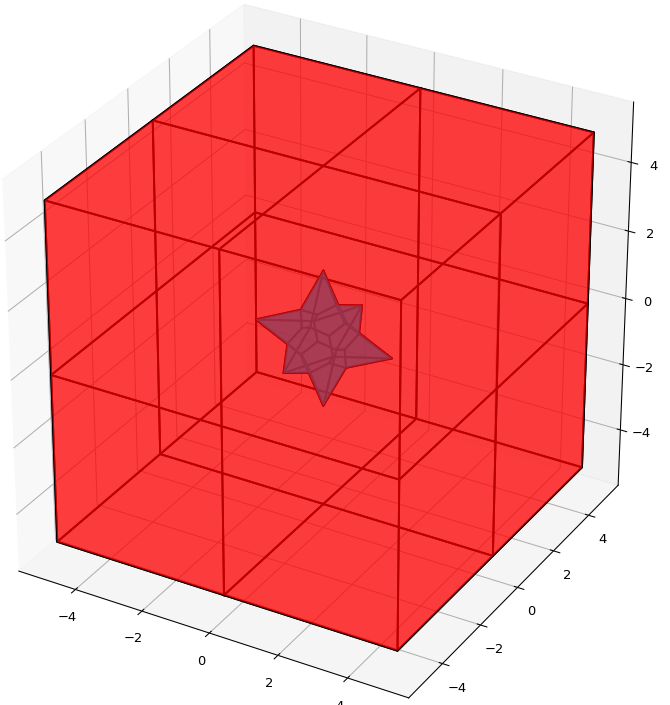
В качестве примера рассмотрим интервальную систему у которой решением является вся область за исключением внутренности:

>>> %matplotlib notebook
>>> inf = np.array([[-1,-2,-2], [-2,-1,-2], [-2,-2,-1]])
>>> sup = np.array([[1,2,2], [2,1,2], [2,2,1]])
>>> A = ip.Interval(inf, sup)
>>> b = ip.Interval([2,2,2], [2,2,2])
>>>
>>> bounds = [[-5, -5, -5], [5, 5, 5]]
>>> vertices = ip.IntLinIncR3(A, b, alpha=0.5, s=0, bounds=bounds, size=(11,11))

Список использованной литературы

[1] И.А. Шарая - Метод граничных интервалов для визуализации полиэдральных множеств решений // Вычислительные технологии, Том 20, No 1, 2015, стр. 75-103.

[2] П.А. Щербина - Метод граничных интервалов в свободной системе компьютерной математики Scilab

[3] С.П. Шарый - Конечномерный интервальный анализ.

Методы для решения квадратных систем

В данном разделе предложены алгоритмы для решения квадратных интервальных систем уравнений.

Метод Гаусса

Метод исключения Гаусса, включая его различные модификации, крайне популярный алгортим в вычислительной линейной алгебре. Поэтому предлагается рассмотреть его интервальную версию, которая также состоит из двух этапов — прямой ход и обратный ход.

Parameters:

• AInterval

  Входная интервальная матрица ИСЛАУ, которая должна быть квадратной.

• bInterval

  Интервальной вектор правой части ИСЛАУ.

Returns:

• outInterval

  Интервальный вектор, который после подстановки в систему уравнений и выполнения всех операций по правилам арифметики и анализа обращает уравнения в инстинные равенства.

Examples:

В качестве примера рассмотрим широко известную интервальную систему, предложенную Бартом-Нудингом:

>>> A = ip.Interval([[2, -2],[-1, 2]], [[4, 1],[2, 4]])
>>> b = ip.Interval([-2, -2], [2, 2])
>>> ip.linear.Gauss(A, b)
interval(['[-5.0, 5.0]', '[-4.0, 4.0]'])

Interval Gauss-Seidel method

def Gauss_Seidel(A, b, x0=None, C=None, tol=1e-12, maxiter=2000)

The iterative Gauss-Seidel method for obtaining external evaluations of the united solution set for an interval system of linear algebraic equations (ISLAE).

Parameters:

• AInterval

  The input interval matrix of ISLAE, which can be either only square.

• bInterval

  The interval vector of the right part of the ISLAE.

• X: Interval, optional

  An initial guess within which to search for external evaluation is suggested. By default, X is an interval vector consisting of the elements [-1000, 1000].

• C: np.array, Interval

  A matrix for preconditioning the system. By default, C = inv(mid(A)).

• tol: float, optional

  The error that determines when further crushing of the bars is unnecessary, i.e. their width is «close enough» to zero, which can be considered exactly zero.

• maxiter: int, optional

  The maximum number of iterations.

Returns:

• outInterval

  Returns an interval vector, which means an external estimate of the united solution set.

Examples:

>>> A = ip.Interval([
        [[2, 4], [-2, 1]],
        [[-1, 2], [2, 4]]
    ])
>>> b = ip.Interval([[1, 2], [1, 2]])
>>> ip.linear.Gauss_Seidel(A, b)
Interval(['[-10.6623, 12.5714]', '[-11.0649, 12.4286]'])

Preconditioning the system with the inverse mean yields a vector of external evaluations that is wider than if a special type of preconditioning matrix were carefully selected in advance. The system presented below is the same system as described above, but preconditioned with a specially selected matrix.

>>> A = ip.Interval([[0.5, -0.456], [-0.438, 0.624]],
                     [[1.176, 0.448], [0.596, 1.36]])
>>> b = ip.Interval([0.316, 0.27], [0.632, 0.624])
>>> ip.linear.Gauss_Seidel(A, b, C=ip.eye(A.shape[0]))
Interval(['[-4.26676, 6.07681]', '[-5.37144, 5.26546]'])

Parameter partitioning methods

def PPS(A, b, tol=1e-12, maxiter=2000, nu=None)

PPS - optimal (exact) componentwise estimation of the united solution set to interval linear system of equations.

x = PPS(A, b) computes optimal componentwise lower and upper estimates of the solution set to interval linear system of equations Ax = b, where A - square interval matrix, b - interval right-hand side vector.

x = PPS(A, b, tol, maxiter, nu) computes vector x of optimal componentwise estimates of the solution set to interval linear system Ax = b with accuracy no more than epsilon and after the number of iterations no more than numit. Optional input argument ncomp indicates a component’s number of interval solution in case of computing the estimates for this component only. If this argument is omitted, all componentwise estimates is computed.

Parameters:

• A: Interval

  The input interval matrix of ISLAE, which can be either square or rectangular.

• b: Interval

  The interval vector of the right part of the ISLAE.

• tol: float, optional

  The error that determines when further crushing of the bars is unnecessary, i.e. their width is «close enough» to zero, which can be considered exactly zero.

• maxiter: int, optional

  The maximum number of iterations.

• nu: int, optional

  Choosing the number of the component along which the set of solutions is evaluated.

Returns:

• out: Interval

  Returns an interval vector, which, after substituting into the system of equations and performing all operations according to the rules of arithmetic and analysis, turns the equations into true equalities.

Examples:

>>> A, b = ip.Neumeier(5, 10)
>>> ip.linear.PPS(A, b)
Interval(['[-0.214286, 0.214286]', '[-0.214286, 0.214286]', '[-0.214286, 0.214286]', '[-0.214286, 0.214286]', '[-0.214286, 0.214286]'])

Список использованной литературы

[1] R.B. Kearfott, C. Hu, M. Novoa III - A review of preconditioners for the interval Gauss-Seidel method // Interval Computations, 1991-1, pp 59-85

[2] С.П. Шарый - Конечномерный интервальный анализ.

[3] S.P. Shary, D.Yu. Lyudvin - Testing Implementations of PPS-methods for Interval Linear Systems // Reliable Computing, 2013, Volume 19, pp 176-196

Методы для решения переопределённых систем

В случаях, когда рассматривается переопределённая интервальная система линейных алгебраических уравнений (ИСЛАУ), то если отбросить некоторые уравнения, чтобы привести систему к квадратному виду, то полученный вектор-решение будет содержать оптимальное оценивания множества решений. Однако такой приём может значительно ухудшить (раздуть) оценку, что, несомненно, является нежелательным. В связи с этим предлагается рассмотреть некоторые алгоритмы для решения переопределённых систем.

Метод Рона

Метод, предложенный Дж. Роном в статье [1], для получения вектора-решения, основан на решении вспомогательного квадратного линейного неравенства. Для получения данного неравенства активно используется наиболее представительная точечная матрица Аc из интеварльной матрицы A, т.е. Ac = mid(A). Реализованный алгоритм является простейшей вариацией алгоритма предложенного в статье и не даёт оптимальное оценивание множества решений.

Parameters:

• AInterval

  Входная интервальная матрица ИСЛАУ, которая может быть как квадратной, так и прямоугольной.

• bInterval

  Интервальной вектор правой части ИСЛАУ.

• tolfloat, optional

  Погрешность, определающая, когда дальнейшее дробление брусов излишне, т.е. их ширина «достаточно близка» к нулю, что может считаться точно нулевой.

• maxiterint, optional

  Максимальное количество итераций для выполнения алгоритма.

Returns:

• outInterval

  Интервальный вектор, который после подстановки в систему уравнений и выполнения всех операций по правилам арифметики и анализа обращает уравнения в инстинные равенства.

Examples:

В качестве примера рассмотрим широко известную интервальную систему, предложенную Бартом-Нудингом:

>>> A = ip.Interval([[2, -2],[-1, 2]], [[4,1],[2,4]])
>>> b = ip.Interval([-2, -2], [2, 2])
>>> ip.linear.Rohn(A, b)
Interval(['[-14, 14]', '[-14, 14]'])

Этот пример также демонстрирует, что решение может быть далеко от оптимального, который в данном случае равен Interval([„[-4, 4]“, „[-4, 4]“]). В качестве второго примера предлагается рассмотреть тестовую систему С.П. Шарого:

>>> A, b = ip.Shary(4)
>>> ip.linear.Rohn(A, b)
Interval(['[-4.34783, 4.34783]', '[-4.34783, 4.34783]', '[-4.34783, 4.34783]', '[-4.34783, 4.34783]'])

В отличие от прошлого примера данный вектор-решение достаточно близок к оптимальному внешнему оцениванию.

Метод дробления решений

Гибридный метод дробления решений PSS, подробно описанный в [2]. PSS-алгортимы предназначены для нахождения внешних оптимальных оценок множеств решений интервальных систем линейных алгебраических уравнений (ИСЛАУ) A x = b.

В качестве базового метода внешнего оценивания в программе используется интервальный метод Гаусса (функция Gauss), если система является квадратной. В случае, если система переопределённая, то применяется простейший алгоритм, предложенный Дж. Роном (функция Rohn). Поскольку задача NP-трудная, то остановка процесса может произойти по количеству пройденных итераций. PSS-методы являются последовательно гарантирующими, т.е. при обрыве процесса на любом количестве итераций приближённая оценка решения удовлетворяет требуемому способу оценивания.

Возвращает формальное решение интервальной системы линейных уравнений. В случае, если оценивать все компоненты нет необходимости, то можно оценить одну любую nu-ю компоненту.

Parameters:

• AInterval

  Входная интервальная матрица ИСЛАУ, которая может быть как квадратной, так и прямоугольной.

• bInterval

  Интервальной вектор правой части ИСЛАУ.

• tolfloat, optional

  Погрешность, определающая, когда дальнейшее дробление брусов излишне, т.е. их ширина «достаточно близка» к нулю, что может считаться точно нулевой.

• maxiterint, optional

  Максимальное количество итераций для выполнения алгоритма.

• nuint, optional

  Выбор номера компоненты, вдоль которой оценивается множество решений.

Returns:

• outInterval

  Интервальный вектор, который после подстановки в систему уравнений и выполнения всех операций по правилам арифметики и анализа обращает уравнения в инстинные равенства.

Examples:

>>> A, b = ip.Shary(4)
>>> ip.linear.PSS(A, b)
interval(['[-4.347826, 4.347826]', '[-4.347826, 4.347826]', '[-4.347826, 4.347826]', '[-4.347826, 4.347826]'])

Возврат интервального вектора решения NP-трудной системы.

>>> A, b = ip.Neumeier(3, 3.33)
>>> ip.linear.PSS(A, b, nu=0, maxiter=5000)
interval(['[-2.373013, 2.373013]'])

Возвращена отдельная компонента. В связи с тем, что в системе Ноймаера параметр theta=3.33 является жёстким условием, необходимо увеличить количество итераций для получения оптимальной оценки.

Список использованной литературы

[1] J. Rohn - Enclosing solutions of overdetermined systems of linear interval equations // Reliable Computing 2 (1996), 167-171

[2] С.П. Шарый - Конечномерный интервальный анализ.

[3] J. Horacek, M. Hladik - Computing enclosures of overdetermined interval linear systems // Reliable Computing 2 (2013), 142-155